How to Solve Questions related to a Syllogism: Tricks and Practice Question

This article titled ‘How to solve questions related to a syllogism: Tricks and practice question’ is written by Aditya Kumar and discusses the methods of solving syllogism based questions.

I. What is a Syllogism?

Syllogism is originally a word given by the Greeks. It means ‘inference’ or ‘deduction’. The problem of syllogism is supposed to be one of the very roots of logic and it has its history dating back to the times of Aristotle and Plato. The term syllogism is applied to the distinctive form of argument that is the application of deductive reasoning. A syllogism includes two premises that are compared against each other in order to infer a conclusion.

Example

1. Statements: All pine trees are coniferous.

All coniferous are beautiful.

Conclusions: All pine trees are beautiful.

Some beautiful are pine trees

II. Type of statements in syllogism

I. ALL A are B

II. Some A are B

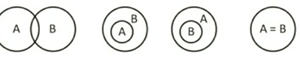
III. Only some A are B

IV. No A is B

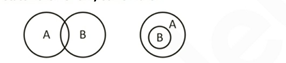
V. Some A are not B

VI. Only some A are not B

EXAMPLE

1. Statements:

All toys are dolls.

No fan is light.

All lights are toys.

Only a few lights are bright.

Conclusions:

1) Only dolls are light.

2) Only light is doll.

1. If conclusion 1 follows
2. If conclusion 2 follows
3. Either conclusion 1 or conclusion 2 follows
4. Neither conclusion 1 nor conclusion 2 follows
5. Both the conclusions follow

Solution

Answer is A

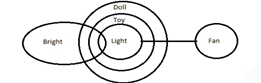
Only dolls are light which means all light are dolls, which is true.

Only light is doll which means all dolls are light, which is false.

So, only 1 follows.

III. Tips and Tricks to Solve Syllogism based Questions

1. Go through all the statements one by one. Understand how you need to draw Venn Diagrams for each of these statements.
2. Try to find out the pattern of the question. Understand how to analyse the conclusion for each statement.
3. The key point you should keep in mind is that you have to attempt the question in a sequential manner.
4. Always keep an eye out for words like ‘some,’ ‘a few,’ ‘all,’ ‘at least,’ and so on. These words serve as the base for answering syllogism questions.
5. The most effective syllogism trick is to answer problems using Venn diagrams. This will help to clarify and simplify the explanation.
6. When answering syllogism questions, never make any assumptions. The data specified in the question is the only data that must be followed when answering the question. When answering questions, there is no need to make any additional assumptions.

IV. Practice question based on syllogism

1. Statements:
   No banana is a plum.
   All plums are oranges.
   All oranges are mangoes.

Conclusions:
All plums are mangoes.
II. At least some mangoes are oranges.

A. Neither I nor II follows

B. Only I follows

C. Either I or II follows

D. Both I and II follow

E. Only II follows

2. Statements:
   All birds are mammals.
   
   No mammal is reptile.
   All reptiles are amphibians.

Conclusions:
All birds are amphibians.
II. Some amphibians are mammals.

A. Neither I nor II follows

B. Only I follows

C. Either I or II follows

D. Both I and II follow

E. Only II follows

3. Statement:
   Some schools are classes.
   Some classes are boy.
   All boy are students.

Conclusions:
I. Some students are classes.
II. All schools being students is a possibility.

A. Neither I nor II follows

B. Only I follows

C. Either I or II follows

D. Both I and II follow

E. Only II follows

4. Statements:
   Some buses are cars.
   No car is red.
   All red are bikes.

Conclusions:
I. Some buses are not bikes.
II. No bike is ship.

A. Neither I nor II follows

B. Only I follows

C. Either I or II follows

D. Both I and II follow

E. Only II follows

5. Statements:
   All cups are blue.
   All plates are cups.
   Some blue are spoons.

Conclusions:
I. All plates being spoons is a possibility.
II. All plates are not saucers.

A. Neither I nor II follows

B. Only I follows

C. Either I or II follows

D. Both I and II follow

E. Only II follows

V. Solutions

1. All plums are oranges (A) + All oranges are mangoes (A) = A + A = All plums are mangoes. Hence, conclusion I follows. All oranges are mangoes – converse – Some mangoes are oranges. Hence, conclusion II follows. Option D is correct.
2. All birds are amphibians. The class ‘birds’ is in Statement 1 and ‘amphibians’ is in Statement 3 and the link or middle term is available in Statement 2 which is an E type statement. Clearly, using these we can’t have an A type conclusion. C1, clearly, doesn’t follow. Checking C2: Some amphibians are mammals. Applying the same logic, we can’t get a positive conclusion using Statement 2 and Statement 3. C2, doesn’t follow either. Option A is correct.
3. Some students are classes. Some classes are boy+ All boy are students = Some classes are students. Clearly, C1 follows. All schools being students is a possibility. Here, no negative statement is given among the statements. Clearly, possibilities between classes do exist. C2 follows as well. Option D is correct.
4. Some buses are not bikes. Here, S1 is I type, S2 is E type, and the class ‘bikes’ is the predicate in S2 which is an A type statement. When we move from S1 to S2, we get a conclusion in O type statement and as we know O type doesn’t make a definite conclusion applying deduction method. No definite conclusion can be derived out of S1, S2 and S3 together. C1, hence, doesn’t follow. No bike is red. Converse of S3 = Some bikes are red. Clearly, C2 doesn’t follow either. Option A is correct.
5. All plates being spoons is a possibility. As there is no negative statement, possibilities between classes do exist. Clearly, C1 follows. All plates are not blue. As there is no negative statement, a negative definite conclusion is not possible. C2, hence, doesn’t follow. Option B is correct.

---

References

1. Analytical reasoning by MK Pandey

2. Jagran Josh, Available Here.

3. SmartKeeda, Available Here.

---

1. Law Library: Notes and Study Material for LLB, LLM, Judiciary and Entrance Exams
2. Legal Bites Academy – Ultimate Test Prep Destination